Quantum Variational Principle

I was going over a book about quantum mechanics this weekend. The book in question is none other than the canonical Claude-Cohen-Tanouji [1]. I remember this book being at my bedside throughout my graduate years. This book may not be as popular as I initially thought in the Anglo-Saxon countries, but it surely was in France and Algeria, where I did most of my studies. Nevertheless, I was reading through the chapter about the perturbative theory, and one of the complements of Chapter XI caught my attention. It was about the variational method as an alternative to the stationary perturbation theory.

Before we go into the subject of this post, let's take a step back and explore what this method is all about. Imagine you have a stable quantum system, with its energy levels and wave functions perfectly described by the Hamiltonian $H_0$ . Now, let's introduce a time-independent perturbation and let call it $V$ , you can imagine this as if you are adding a gentle ripple to the potential landscape of our system. This is where stationary perturbation theory comes in. It helps us understand the shifts that occur in our system's energy levels, $E_n$ , and wave functions, $ϕ_n$ . To calculate these shifts, we expand the perturbed Hamiltonian, $H = H_0 + V$ , and use our QM toolkit to analyse the resulting changes. The beauty of stationary perturbation theory lies in its ability to provide accurate approximations of complex systems that are difficult to solve exactly.

But there is a catch! Perturbation theory is of no help unless we know the exact solutions to a problem whose Hamiltonian is sufficiently similar. So, what do we mean by that? Perturbation theory in quantum mechanics is usefull only when we have a Hamiltonian of a simple system that we can solve exactly and is quite similar to the more complex Hamiltonian $H$ we are interested in. The theory assumes that the difference between H and $H_0$ is small (hence the term perturbation), so $H_0$ serves as a good approximation. Suppose $H_0$ is not sufficiently similar to $H$ . In that case, the perturbation theory may not provide accurate or meaningful results, as it assumes that the perturbation only causes slight deviations from the known solution of $H_0$ .

This is where the variational method becomes in. This method estimates the ground state energy $E_0$ when such exact solutions are unavailable. Instead of working with a fixed set of unperturbed states, one guesses a trial state $|\psi\rangle$ , which may be expanded in terms of the basis set of eigenstates $\phi_n$ of the Hamiltonian $H$ . In other words, it is possible to determine the ground state without the explicit solution of the Schrödinger equation by requiring that its energy be the lowest of all possible energies for all possible wave functions.

To understand this, we consider an arbitrary Hamiltonian $H$ and demand that its spectrum have a lower limit. This means that it has the lowest, non-degenerate energy eigenvalue:

\begin{align} H|\phi_n\rangle = E_n |\phi_n\rangle &;& \nonumber \\ E_n > E_0 &;& ~(n\neq 0) \nonumber \end{align}

We can write the following by expending any arbitrary normalised wave function $\psi$ into an eigenfunctions of $H$ .

|\psi\rangle = \sum_{n}c_n|\phi_n\rangle \text{ with, } \sum_{n}|c_n|^2 = 1

We can then easily demonstrate by calculating the mean energy of $|\psi\rangle$ that you have a lower limit $E_0$ that corresponds to the ground state

\begin{align} \langle\psi|H|\psi\rangle &= \sum_n E_n |c_n|^2 \nonumber \\ &\geq E_0 \sum_n |c_n|^2 = E_0 \nonumber \end{align}

It is evident from these results that every other state $|\psi\rangle$ that differs from the grounds state has an energy higher than $|0\rangle$ . We can write this in more condensed manner in the form of

E_0 = min_{|\psi\rangle \in \mathcal{H}} \left[\frac{\langle \psi|H|\psi\rangle}{\langle\psi|\psi\rangle}\right]

Here $|\psi\rangle \in \mathcal{H}$ indicates that $|\psi\rangle$ is an element of the Hilbert space of H. By simply writing the problem in this fashion, we are explicitly saying that finding energy of the ground state has become a variational problem that is, the expression in brackets has to be stationary ( $\delta E[\psi] = \delta(\langle \psi|H|\psi\rangle/\langle \psi|\psi\rangle)=0$ ) to be a necessary condition for the extremum (or minimum in our case here). We can go on by doing a variational analysis to prove that this statement is equivalent to Schrödinger's formalism. This can be found in the book mentioned above. This variational principle is known as Ritz's variational method which starts by considering a "trial ket'', $|\psi(x, \theta_1, ..., \theta_n)\rangle$ which is made to depend on real parameters $\theta_i$ , then we can search for the minimum $E_\psi( \theta_1, ..., \theta_n)$ by doing

\frac{\partial}{\partial \theta_i} E_\psi( \theta_1, ..., \theta_n) = 0

This guarantees us the upper approximation for the energy in the ground state.

Using a Quantum Computer

In quantum computing, the variational principle of quantum mechanics is used to define a class of algorithms Variational Quantum Eigensolvers (VQEs). From what we have seen above, the variational principle tells us that the ground state $|\psi\rangle$ minimises the expectation $\langle H\rangle = \langle\psi|H|\psi\rangle$ of the Hamiltonian H of the system. The idea of VQEs is to use a parametrised ansatz $W (\theta)$ to prepare a state $|\psi(\theta)⟩ = W (\theta)$ . Instead of finding the ground state $|\psi\rangle$ , we find the parameters θ that minimise the above expectation which means finding the energy. In other words, we use the expectation of the Hamiltonian as the cost function that we can now write as fellow.

C(\theta) = \langle \psi(\theta)|H|\psi(\theta)\rangle

In a variational quantum algorithm. The best approximation $\psi(\hat \theta)\rangle$ to the ground state given an ansatz $|\psi\rangle$ minimises the cost function $C(\theta)$ over all values of parameters $\theta$ . The quantum computer determines the expected value of the energy. This is typically computed by a quantum algorithm. However, the energy minimisation is performed with a classical optimisation algorithm. For this reason, VQE is considered a hybrid classical-quantum algorithm.

PennyLane example

Let's implement a simple example in pennylane and see how we can find the ground state. The simplest quantum system we can think of is the quantum harmonic oscillator (QHO), let us first define its Hamiltonian.

H_{QHO} = -\frac{\hbar}{2m}\frac{d^2}{dx^2} + \frac{1}{2}m\omega^2x^2

A clever trick in quantum mechanics is to express this Hamiltonian in terms of annihilation and creation operators, $\hat a^\dagger$ and $\hat a$ . This transformation simplifies our equation to:

H_{QHO} = \hbar \omega (a^\dagger a + \frac{1}{2})

The ground state energy of the QHO is analytically found to be $E_{0} = \frac{1}{2}\hbar \omega$ . But how does this translate in the realm of quantum computing? This is where PennyLane comes into play, offering a platform to apply the variational method in finding this ground state.

One of the key features of PennyLane is its support for fermionic creation and annihilation operators, essential in quantum mechanics. These operators are easily accessible in PennyLane through the FermiC and FermiA functions:

from pennylane import FermiC, FermiA
 
w = 1.0 
H = w * (FermiC(0) * FermiA(0) + 0.5)

This is not enough, though. We need to map this Hamiltonian to a qubit basis, a necessary step in quantum computing. This is where the Jordan-Wigner transformation comes into play, another gem in PennyLane’s toolbox.

from pennylane import jordan_wigner  
hamiltonian = jordan_wigner(H)
# out: Identity(wires=[1]) + ((-0.5+0j)*(PauliZ(wires=[1])))

The next step is to define quantum Circuit Ansatz. It's a variational circuit designed to navigate a wide range of quantum states. In this instance, a simple single qubit circuit with an X rotation suffices. We then define the cost function $C(\theta)$ . This function computes the expectation value of the Hamiltonian. In Pennylane, this is done using the @qml.qnode decorator to create quantum nodes that return the expectation value.

dev = qml.device('default.qubit', wires=1)
 
@qml.qnode(dev)
def ansatz(theta): 
  qml.RX(theta, wires=0)
  return qml.expval(H)
 
def cost(theta): 
  return circuit(theta)

Finally, the optimisation! We will use classical optimisation algorithms like iconic gradient descent to find the parameter $\theta$ that minimises the expectation value $C(\theta)$ . This process iteratively adjusts the parameters of our quantum circuit to approximate the ground state energy. The minimum energy obtained through optimisation approximates the ground state energy of the quantum harmonic oscillator.

Finally, the optimisation! Employing a classic gradient descent algorithm, we seek the parameter $\theta$ that minimises $C(\theta)$ . This process iteratively adjusts the parameters of our quantum circuit to approximate the ground state energy. The minimum energy obtained through optimisation approximates the ground state energy of the quantum harmonic oscillator.

params = np.random.random([nqubits], requires_grad=True)
opt = qml.GradientDescentOptimizer(stepsize=0.5)
 
steps = 20
costs_gd = []
for i in range(steps):
    costs_gd.append(cost(params))
    params = opt.step(cost, params)
    
print("Ground state energy:", cost(params))

And voilà! If the cosmos aligns in our favour, the output hovers around 0.5. We can also plot the progress of the loss function as well as the value of the parameter $\theta$ at every step. Only 20 iterations are enough to find the ground state.

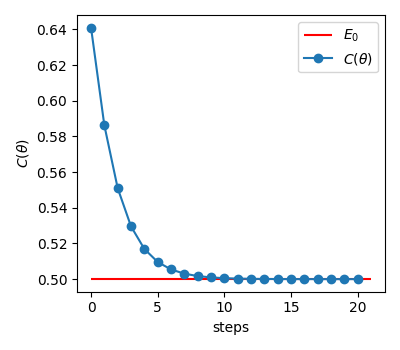
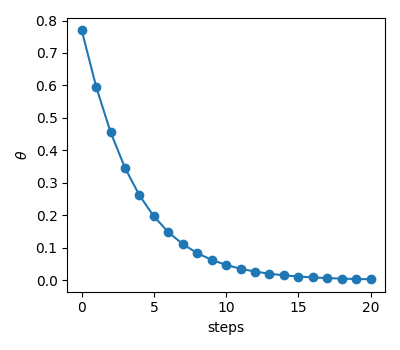
This elegant example is just the tip of the quantum iceberg. PennyLane harbours a treasure trove of more complex examples that use VQE to solve quantum chemistry problems and very interesting demos that deserve exploration.

References

[1]

C. Cohen-Tannoudji, B. Diu, F. Laloë, Quantum mechanics; 1st ed., (1977). https://cds.cern.ch/record/101367.