Picture this: the majestic Alps, a setting not just for breathtaking views but also for breathtaking science. The Les Houches 2019 workshop brought together brilliant minds to probe deeper into the Higgs boson's secrets. It is definitively one of my favourite workshops so far. During this event, many set to study various fundamental questions, among wich: What are the charge (C) and the parity (P) symmetries of the Higgs boson?

In the Standard Model (SM) of particles physics, the Higgs boson interactions preserve the CP symmetries. Any deviation from the expected CP symmetries could hint at physics beyond the Standard Model (BSM). That's what makes this study so riveting!
CP violation and VBF
The Vector Boson Fusion (VBF) production process at the LHC (Large Hadron Collider). It's the second most copious way Higgs boson is produced, and it has a unique fingerprint: two forward tagging jets. These jets form like a lighthouse whose beams pointing into opposite directions in the detector leading us to a cleaner signal sample and better background rejection.
Now, let's talk physics. The interaction of the Higgs boson with two spin-one gauge bosons is where the action is. The tensor structure of this HVV vertex is sensitive to the CP properties of the Higgs boson. The most general tensor structure describing the interaction of the Higgs boson with two spin-one gauge boson which contributes to the VBF production mode can be written as
where and are the four-momenta of the two fusing gauge bosons . The scalar represents the SM contribution to the coupling, while the form factors and represent CP-even and CP-odd amplitudes respectively. An anomaly in couplings can manifest itself as a deviation of these parameters from their SM values (which are and ).
One of the coolest tools in this study is the azimuthal angle between the two tagging jets (). It's not just a number; it's a key to differentiating between the form factors. But, there's a catch! If CP-even and CP-odd couplings of similar strength are present, their effects might cancel each other out (see Ref. [1] [2]). To tackle this, the study introduces a clever twist in defining to highlight the interference effects. It's like adding vinegar to french fries, it makes all the difference!
If and are the four-momenta of the two proton-beams and and the four momenta of the two tagging jets from VBF, then
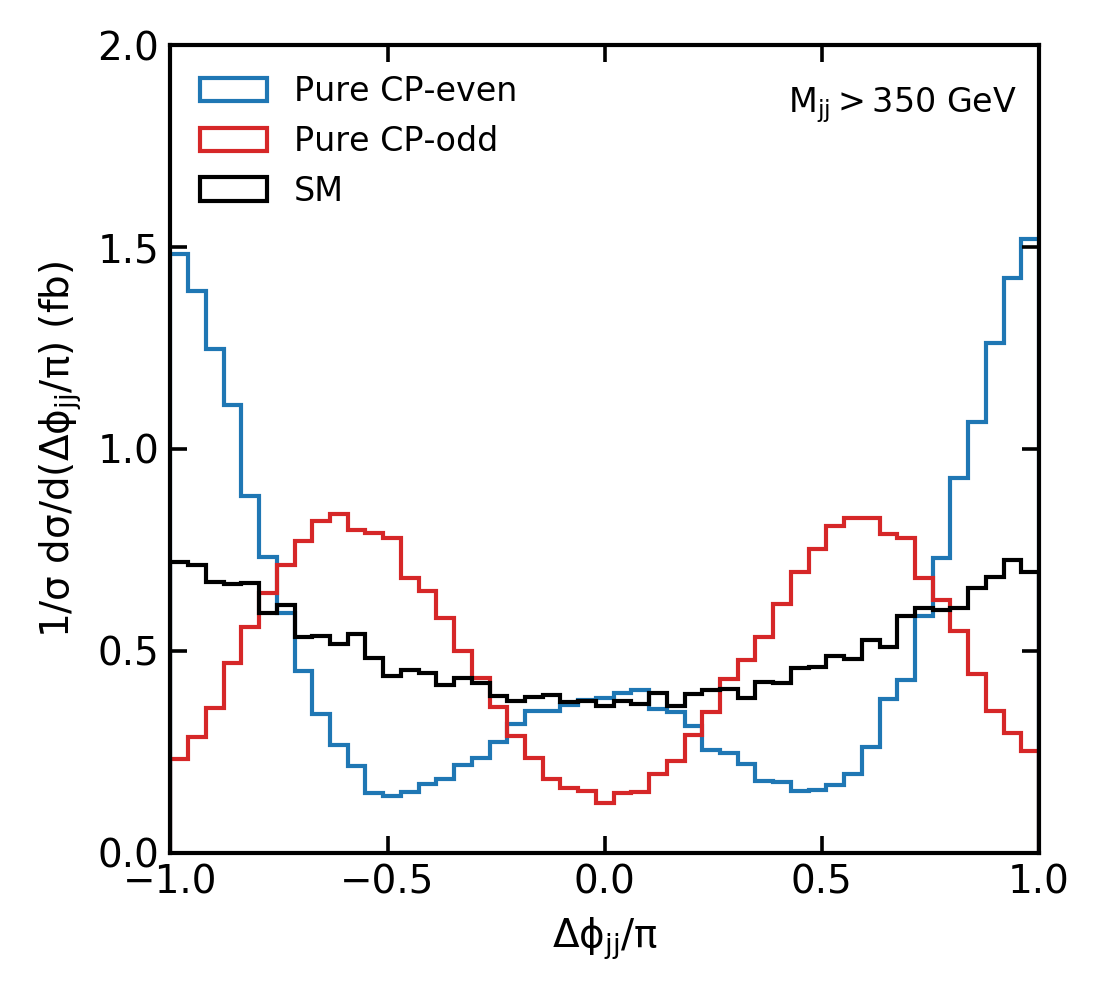
and denotes the four-momenta (azimuthal angles) of the two tagging jets, where () points to the same detector hemisphere as (). Such ordering removes ambiguity in the standard definition of . The ratio of the form factors can directly be measured by determining the minimum of the distribution. The typical distribution of purely CP-odd, CP-event and SM couplings are shown in the following figure,
Redefining STXS Bins
The Simplified Template Cross Sections (STXS) framework [3], evolving from signal strength measurements in Run1, has been adopted in various ATLAS and CMS analyses with a limited bin number. With increasing LHC data, the necessity to examine narrow kinematic areas for beyond the Standard Model (BSM) deviations becomes evident. This research suggests enhancing Stage 1.1 binning [4] through the signed observable, aiming to detect the Higgs boson's elusive CP characteristics.
Higgs boson simulations, involving anomalous HVV couplings, are generated under both scalar and pseudo-scalar assumptions using JHUGEN [5] [6] [7]. To accurately depict final state particle recoil due to QCD radiation, JHUGEN [8] is integrated with Pythia. The Higgs boson remains undecayed in these simulations, with its mass fixed at M_H=125 GeV.
The STXS approach for Stage 1.1, as delineated, categorises the VBF topology starting from an invariant mass threshold of . Subsequently, it divides events based on the Higgs boson's transverse momentum, followed by further segmentation based on and , focusing on distinguishing exclusive 2-jets and inclusive 3-jets categories.
For non-SM contribution assessment, the signal distribution for a specific observable x is modelled as a synthesis of components from SM-like and anomalous amplitudes, including their interference effects [5] [9]
where is template histogram or probability of pure term, and describes the interference between the two terms. Three values of the anomalous coupling are introduced 0.1%, 1% and 10%.
We would like to look at signed in different bins of the STXS stage 1.1 bins definition. For this study, we decided to merge the bins above , as the CP-phase has low dependency on the as well as for . The split at is however kept as it was proven to be sensitive to BSM [4]. The corresponding azimuthal angle distributions are shown below,
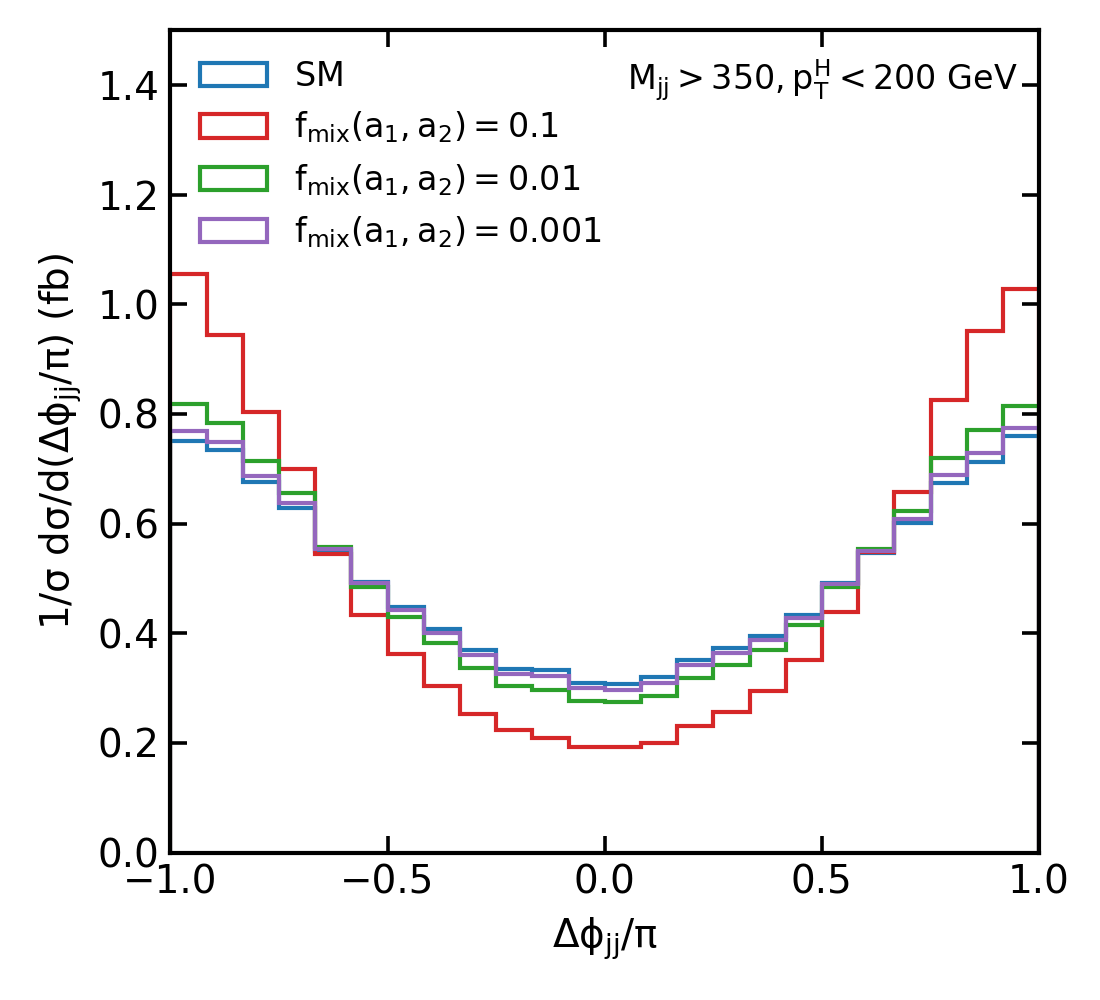
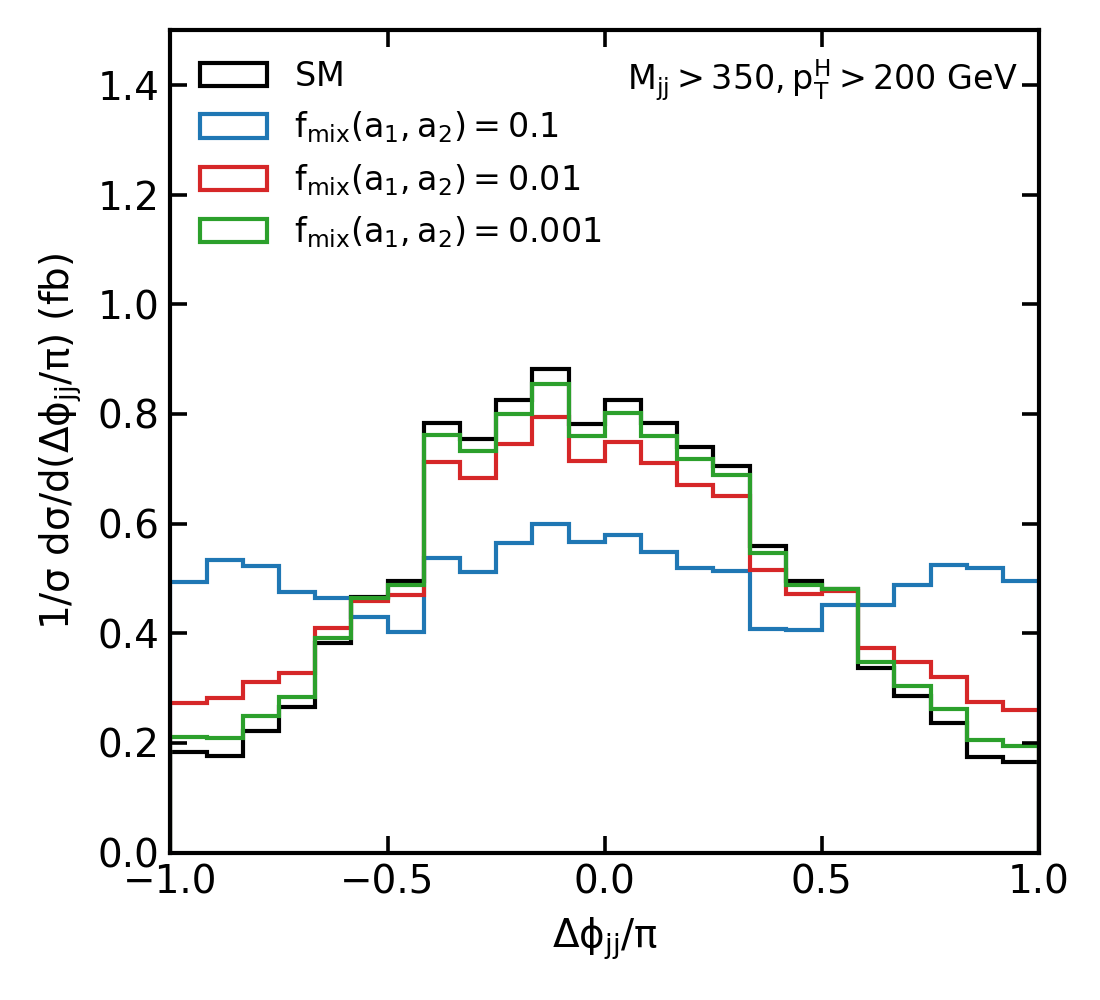
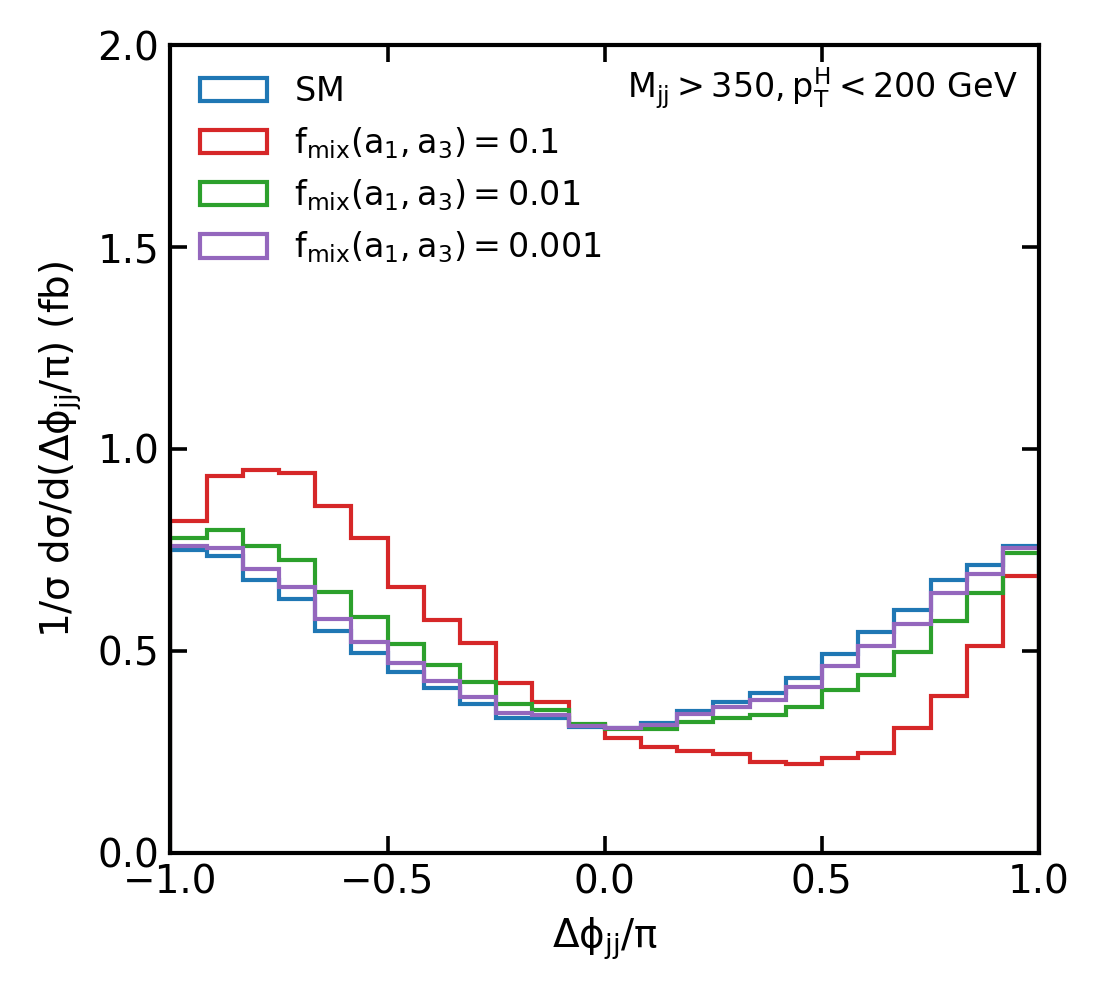
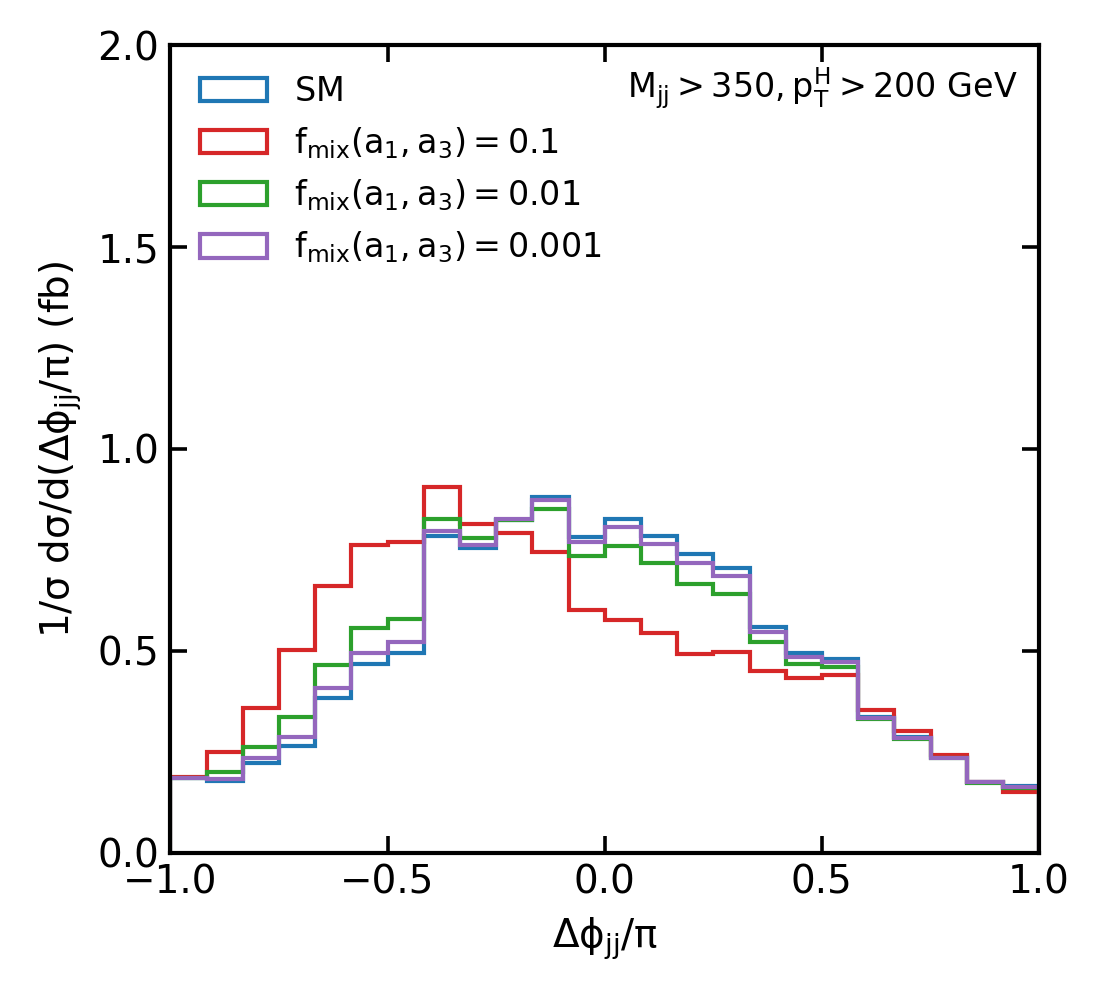
Figure 2: Normalised distributions of the jet-jet azimuthal angle difference as defined in for various mixed CP scenarios between SM and CP-even (a, b) and CP-odd (c, d) couplings. Colours represents different mixing strength values .
In exploring the nuances of CP violation in the Higgs sector, we delve into the intriguing patterns emerging in the distributions. For CP-even coupling, the interference term mirrors the phase of the Standard Model (SM) distribution, as clearly illustrated in Figure. 2:a and Figure. 2:b.. Intriguingly, the most notable deviations from the expected distribution are observed at both the extremities and the midpoint. This effect becomes more pronounced in the high transverse momentum () region, particularly above 200 GeV. By segmenting the data into four distinct bins—ranging from to with divisions at and —we can effectively capture any CP-even deviations from the SM predictions across both high and low scenarios.
Conversely, the CP-odd interference exhibits a fascinating shift in the phase towards negative values. Considering the inherent symmetry in the SM's distribution, any observed asymmetry could be attributed to a parity-odd coupling, specifically the term. This phenomenon is depicted in Figure. 2:c and Figure. 2:d. Here, we observe a phase change in the amplitude at , particularly in the low bin. To better capture these subtleties, a refined binning approach that includes a split at is proposed. This would allow for a more precise measurement of asymmetries in the cross-section between positive and negative bins, potentially unveiling any CP-odd anomalies.
This methodology of defining CP-sensitive bins is not limited to one specific scenario. It can be equally applied to other production modes, notably in stage 1.1, including gluon-fusion and Higgsstrahlung processes. For the Higgsstrahlung process, similar patterns are observed in the HVV vertex. Here, can be particularly insightful for events where the Higgs is accompanied by two jets and the dijet mass () is less than 120 GeV. This approach opens up new avenues for investigating CP violation and its manifestations in various production modes, contributing significantly to our understanding of the Higgs sector.
Conclusion
So, what have we got here? we have presented an extension to the VBF STXS stage 1.1 to include CP-sensitive bins based on the signed observable. We have demonstrated that the usage for such observable is largely independent of the form factor and allows the probe of the HVV coupling. A binning of is proposed under bins above in both high and low branches.

